التابع اللوغاريتمي
( T: Logaritma Fonksiyonu )
(E: Logarithm Function)
وهو التابع العكسي للتابع الأسي \(e^x\) ويعطى بالشكل:
\[f:]0,+\infty[ ~~\rightarrow ~~]-\infty,+\infty[\]
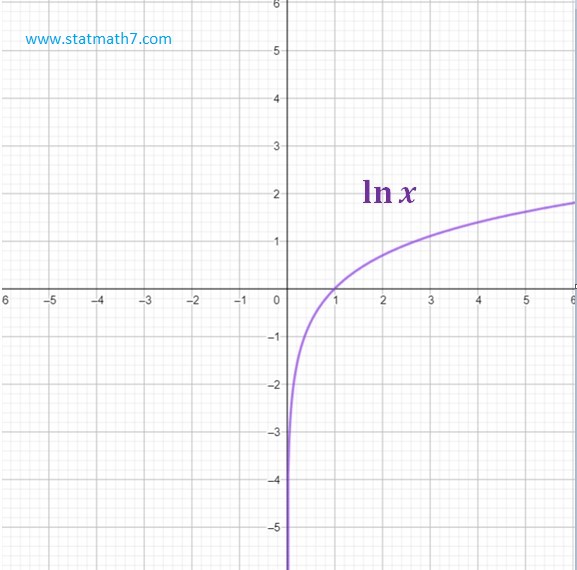
\[f(x)=\ln x\]
نلاحظ أن:
\[\lim_{x\overset{\gt}{\rightarrow} 0}\ln x=-\infty~~,~~\lim_{x\rightarrow +\infty}\ln x=+\infty\]
مقالات ذات صلة:
تعريف المتتالية العددية
تقارب متتالية
تعريف المتتالية الجزئية
تعريف المتتالية المحدودة
متتالية كوشي
العمليات على النهايات
مبرهنة الحصر للمتتاليات
العمليات على النهايات
حالات عدم التعيين
قاعدة أوبيتال
نهاية تابع
الاستمرار
الاشتقاق
تعريف التابع الأسي \(e^x\)
معيار المقارنة للمتسلسلات
معيار المقارنة للمتسلسلات(E: The Comparison Test)(T: Karşılaştırma Testi) لتكن لدينا المتسلسلتان:\[\…
المعيار الصفري لتقارب متسلسلة
المعيار الصفري لتقارب متسلسلة لتكن لدينا المتسلسلة:\[\sum^\infty_{k=1}a_k\]إذا كان :\[\lim_{k \right…
المتسلسلة الهندسية
المتسلسلة الهندسية(E: Geometric Series)(T: Geometrik Seri ) وهي متسلسلة من الشكل:\[\sum^\infty_{k=1}…
المتسلسلة الريمانية
المتسلسلة الريمانية(E: Harmonic Series)(T: Harmonik Seri ) وهي متسلسلة من الشكل:\[\sum^\infty_{k=1}\…
العمليات على المتسلسلات
العمليات على المتسلسلات(E: Operations on Series)(T: Seriler Üzerinde İşlemler) لتكن لدينا المتسلسلتا…
