تعريف التابع المثلثي \(\sin x \)

التابع المثلثي \(\sin x\)
( \(\sin x\) T: Trigonometrik Fonksiyon )
( \(\sin x\) E: Trigonometric Function )

هو تابع بالشكل:
\[f:]-\infty,+\infty[ ~~\rightarrow ~~[-1,+1]\]
\[f(x)=\sin x\]
نلاحظ أن:
\[\lim_{x\rightarrow -\infty}\sin x ~~غير موجودة~~,~~\lim_{x \rightarrow +\infty}\sin x ~~غير موجودة\]

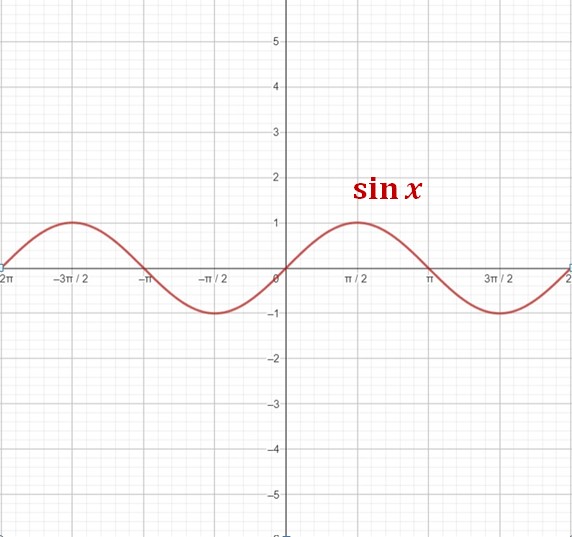
التابع \(\sin\) بدلالة التوابع المثلثية الأخرى:
\[\sin x=\sqrt{1-\cos^2 x}\]
\[\sin x=\frac{\tan x}{\sqrt{1+\tan^2 x}}\]
\[\sin x=\frac{1}{\sqrt{1+\cot^2 x}}\]
\[\sin x=\frac{\sqrt{\sec^2 x-1}}{\sec x}\]
\[\sin x=\frac{1}{\csc x}\]

مقالات ذات صلة:
العمليات على النهايات
مبرهنة الحصر للمتتاليات
العمليات على النهايات
حالات عدم التعيين
قاعدة أوبيتال
نهاية تابع
الاستمرار
الاشتقاق
تعريف التابع الأسي \(e^x\)
تعريف التابع اللوغاريتمي \(\ln x\)