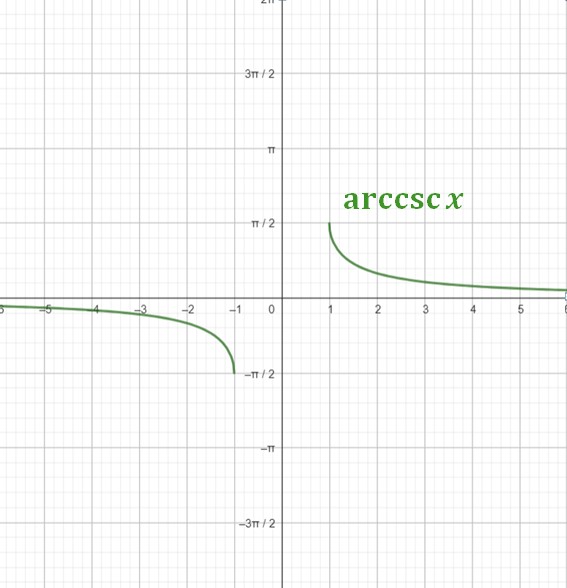
التابع المثلثي العكسي \(arccsc ~x\)
( \(arccsc ~x\) T: Ters Trigonometrik Fonksiyon )
( \(arccsc ~x\) E: Inverse Trigonometric Function )
هو التابع العكسي لتابع الـ \(\csc \):
\[f: ]-\infty,-1[\cup[1,+\infty[~~\rightarrow ~~[-\frac{\pi}{2},0[\cup ]0,\frac{\pi}{2}]\]
\[f(x)=arccsc~ x=\csc^{-1} x\]
نلاحظ أن:
\[\lim_{x \rightarrow -\infty} arccsc ~x =0~,~\lim_{x \rightarrow +\infty} arccsc ~x =0\]
\[ arccsc~(-1)=-\frac{\pi}{2}~~,~~arccsc~(1)=\frac{\pi}{2}\]
مقالات ذات صلة:
تعريف التابع الأسي \(e^x\)
تعريف التابع اللوغاريتمي \(\ln x\)
تعريف التابع المثلثي \(\sin x \)
تعريف التابع المثلثي \(\cos x \)
تعريف التابع المثلثي \(\tan x\)
تعريف التابع المثلثي \(\cot x\)
تعريف التابع المثلثي \(\sec x\)
تعريف التابع المثلثي \(\csc x\)
تعريف التابع المثلثي العكسي \(\arcsin x\)
تعريف التابع المثلثي العكسي \(\arccos x\)
تعريف التابع المثلثي العكسي \(\arctan x\)
تعريف التابع المثلثي العكسي \(arccot ~x\)
تعريف التابع المثلثي العكسي \(arcsec ~x\)
معيار المقارنة للمتسلسلات
معيار المقارنة للمتسلسلات(E: The Comparison Test)(T: Karşılaştırma Testi) لتكن لدينا المتسلسلتان:\[\…
المعيار الصفري لتقارب متسلسلة
المعيار الصفري لتقارب متسلسلة لتكن لدينا المتسلسلة:\[\sum^\infty_{k=1}a_k\]إذا كان :\[\lim_{k \right…
المتسلسلة الهندسية
المتسلسلة الهندسية(E: Geometric Series)(T: Geometrik Seri ) وهي متسلسلة من الشكل:\[\sum^\infty_{k=1}…
المتسلسلة الريمانية
المتسلسلة الريمانية(E: Harmonic Series)(T: Harmonik Seri ) وهي متسلسلة من الشكل:\[\sum^\infty_{k=1}\…
العمليات على المتسلسلات
العمليات على المتسلسلات(E: Operations on Series)(T: Seriler Üzerinde İşlemler) لتكن لدينا المتسلسلتا…
