تعريف التابع القطعي العكسي \(arccsch~x\)

التابع القطعي العكسي \( arccsch~ x\)
( \(arccsch ~x\) T: Ters Hiperbolik Fonksiyon )
( \(arccsch~ x\) E: Inverse Hyperbolic Function )

وهو التابع العكسي لتابع الـ \(csch ~x\) يعطى بالشكل:
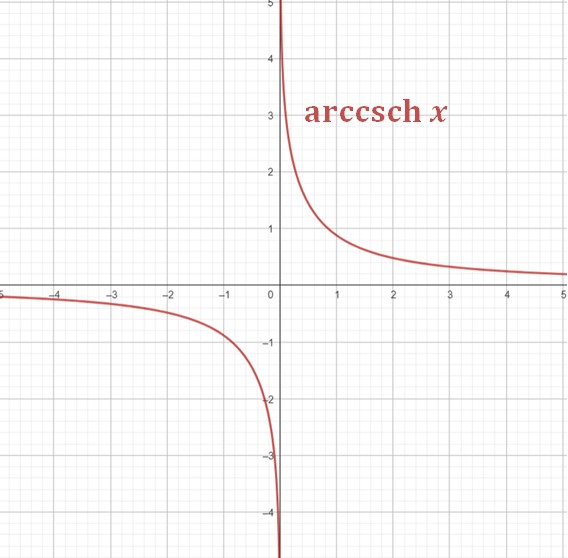
\[f: ]-\infty,0]\cup]0,+\infty[~~\rightarrow~~ ]-\infty,0]\cup]0,+\infty[\]
\[f(x)=arccsch~ x=csch ^{-1} ~x\]
نلاحظ أن:
\[\lim_{x\rightarrow -\infty} arccsch~ x =0~~,~~\lim_{x\rightarrow +\infty} arccsch~ x =0\]
\[\lim_{x\overset{\lt}\rightarrow 0} arccsch~ x =-\infty~~,~~\lim_{x\overset{\gt}\rightarrow 0} arccsch~ x =+\infty\]

مقالات ذات صلة:
تعريف التابع الأسي \(e^x\)
تعريف التابع اللوغاريتمي \(\ln x\)
تعريف التابع المثلثي \(\sin x \)
تعريف التابع المثلثي \(\cos x \)
تعريف التابع المثلثي \(\tan x\)
تعريف التابع المثلثي \(\cot x\)
تعريف التابع المثلثي \(\sec x\)
تعريف التابع المثلثي \(\csc x\)
تعريف التابع المثلثي العكسي \(\arcsin x\)
تعريف التابع المثلثي العكسي \(\arccos x\)
تعريف التابع المثلثي العكسي \(\arctan x\)
تعريف التابع المثلثي العكسي \(arccot ~x\)
تعريف التابع المثلثي العكسي \(arcsec ~x\)
تعريف التابع المثلثي العكسي \(arccsc ~x\)
تعريف التابع القطعي \(\sinh x\)
تعريف التابع القطعي \(\cosh x\)
تعريف التابع القطعي \(\tanh x\)
تعريف التابع القطعي \(\coth x\)
تعريف التابع القطعي \(sech ~x\)
تعريف التابع القطعي \(csch~ x\)
تعريف التابع القطعي العكسي \( arcsinh~ x\)
تعريف التابع القطعي العكسي \( arccosh~ x\)
تعريف التابع القطعي العكسي \( arctanh~ x\)
تعريف التابع القطعي العكسي \( arccoth~ x\)
تعريف التابع القطعي العكسي \( arcsech~ x\)