تحليل عقدي

سعة عدد عقدي
(T: Karmaşık Sayının Argümenti)
(E: Argument of a Complex Number)

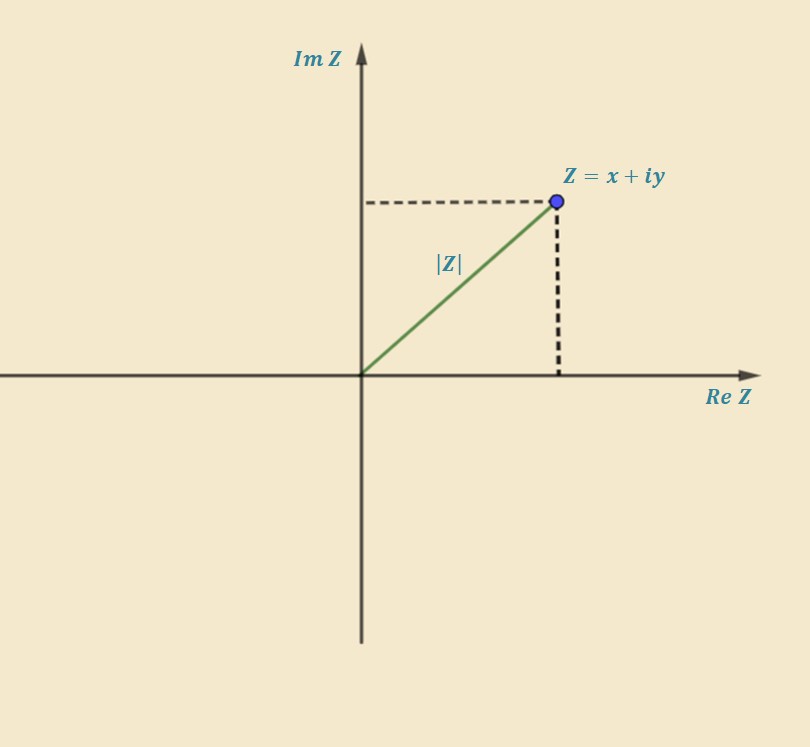
ليكن لدينا العدد العقدي بالشكل الديكارتي:
\[Z=x+iy \]
رأينا انه يمكن تمثيل العدد العقدي في مستوي نظام الاحداثيات الديكارتية. إن سعة العدد العقدي \( Z\) (T: Karmaşık Sayının Argümenti) (E: Argument of a Complex Number) هو الزاوية المحصورة بين المتجه والقسم الموجب من المحور الحقيقي \(Re Z\) ونرمز له بالرمز \(arg Z\) . يمكن توضيح سعة العدد العقدي هندسياُ بالشكل التالي:

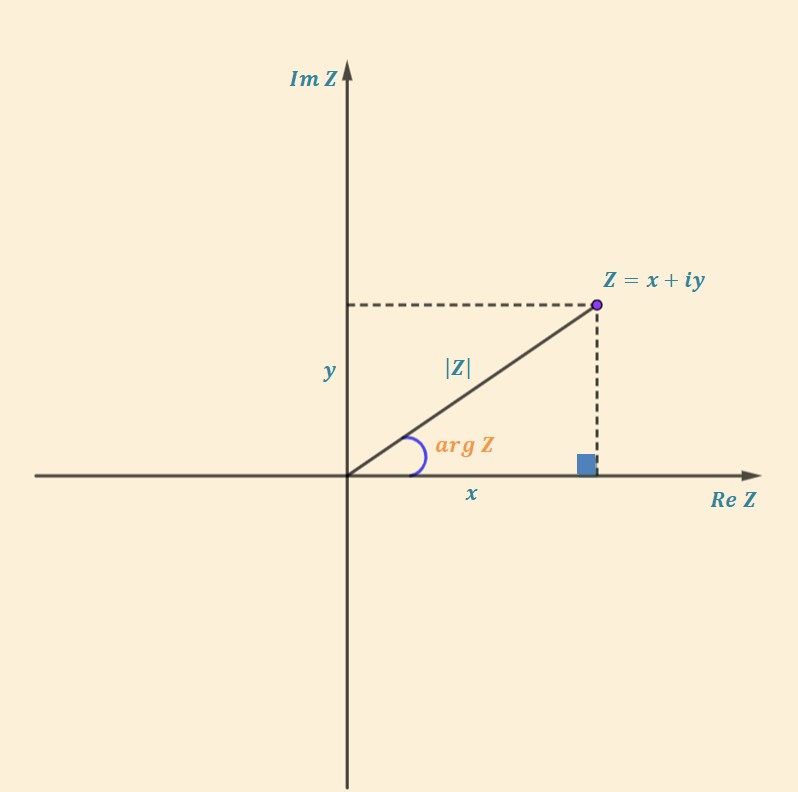
نلاحظ من الرسم السابق أن:
\[\sin (arg Z) =\frac {y}{|Z|}, Z \neq 0 \]
\[\cos (arg Z) =\frac {x}{|Z|}, Z \neq 0 \]
\[\tan (arg Z) =\frac {y}{x}, x \neq 0 \]
نستطيع حساب سعة العدد العقدي \(Z=x+iy\) عن طريق التابع العكسي لتابع الظل من خلال العلاقة:
\[argZ=
\begin {cases}
\arctan (\frac{y}{x}), & x\gt0,y\neq0\\
\arctan (\frac{y}{x})+\pi, & x\lt0,y\ge0\\
\arctan (\frac{y}{x})-\pi, & x\lt0,y\lt0
\end{cases}
\]

مقالات ذات صلة:
مجموعة الأعداد العقدية
الشكل الديكارتي للعدد العقدي
المعنى الهندسي للعدد العقدي
مرافق العدد العقدي
طويلة العدد العقدي

طويلة عدد عقدي
(T: Karmaşık Sayının Modülü)
(E: Modulus of a Complex Number)

ليكن لدينا العدد العقدي بالشكل الديكارتي:
\[Z=x+iy \]
إن طويلة العدد العقدي \( Z\) (T:Karmaşık Sayının Modülü ) (E:Modulus of a Complex Number) هو العدد \( \sqrt{x^2+y^2}\) ونرمز له بالرمز \(| Z|\) إي أن:
\[| Z|=\sqrt{x^2+y^2}\]. يمكن توضيح طويلة العدد العقدي هندسياُ بالشكل التالي:

مقالات ذات صلة:
مجموعة الأعداد العقدية
الشكل الديكارتي للعدد العقدي
مرافق العدد العقدي