المعنى الهندسي للأعداد العقدية
المعنى الهندسي للأعدادالعقدية
(T: Karmaşık Sayıların Geometrik Gösterimi)
(E: The Geometric View of Complex Numbers)
يمكن أن نكتب العدد العقدي \(Z=(x,y)\) بالشكل الديكارتي:
\[Z=x+iy\]
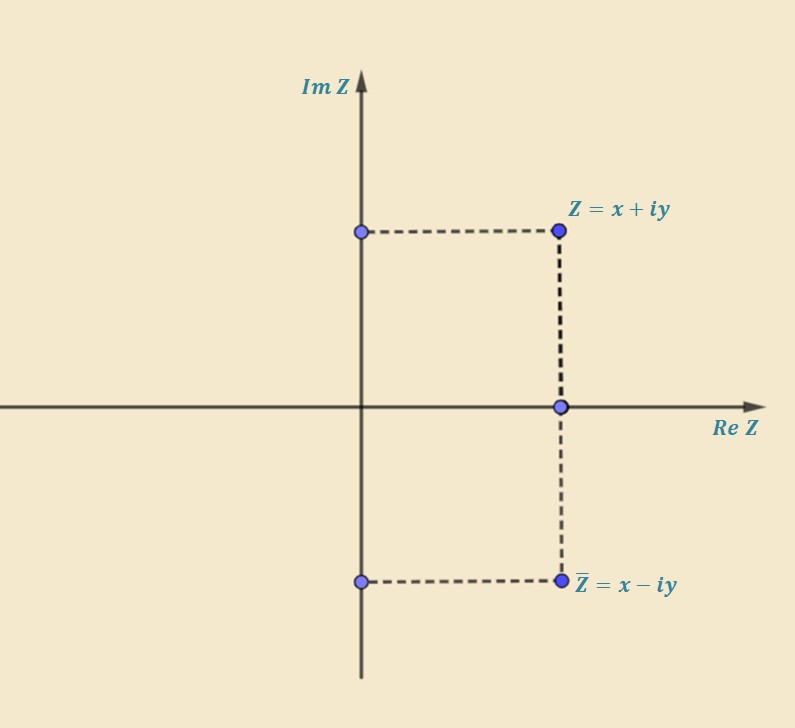
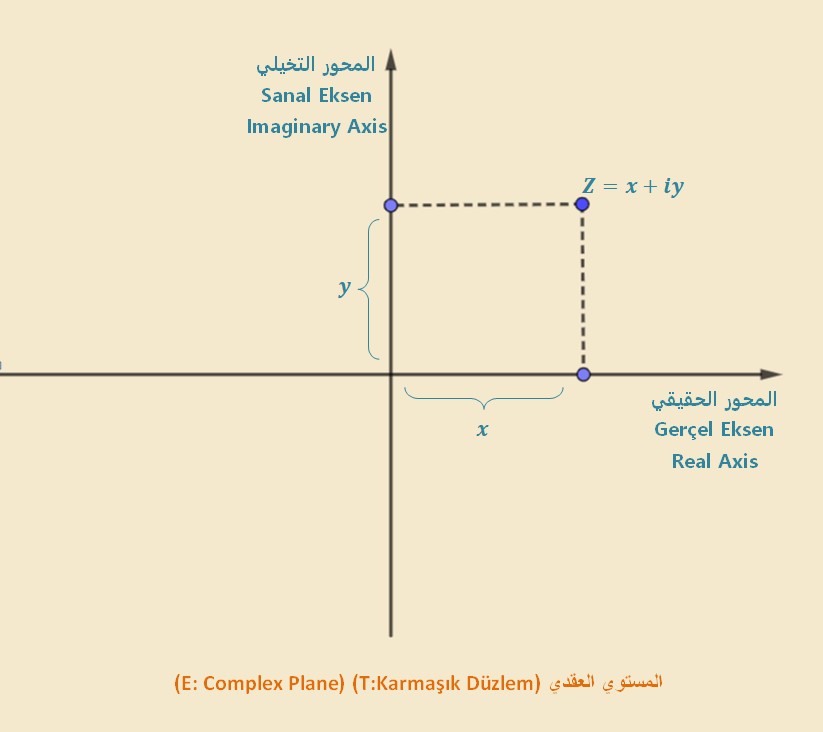
بما أنه يمكن كتابة كل عدد عقدي على شكل ثنائية \((x,y)\) وبالتالي يمكن تمثيل كل عدد عقدي \(Z=x+iy\) في مستوي نظام الاحداثيات الديكارتية (T: Kartezyen Koordinat Sistemi) (E: Cartesian Coordinate System) حيث يكون هذا المستوي مؤلف من محور حقيقي (T: Gerçel Eksen) (E: Real Axis) ومحور تخيلي (T: Sanal Eksen) (E: Imaginary Axis) ويسمى هذا المستوي بالمستوي العقدي (T: Karmaşık Düzlem) (E: Comlex Plane) كما هو موضح في الشكل التالي:
مقالات ذات صلة:
مجموعة الأعداد العقدية
الشكل الديكارتي للعدد العقدي
مرافق العدد العقدي
معيار المقارنة للمتسلسلات
معيار المقارنة للمتسلسلات(E: The Comparison Test)(T: Karşılaştırma Testi) لتكن لدينا المتسلسلتان:\[\…
المعيار الصفري لتقارب متسلسلة
المعيار الصفري لتقارب متسلسلة لتكن لدينا المتسلسلة:\[\sum^\infty_{k=1}a_k\]إذا كان :\[\lim_{k \right…
المتسلسلة الهندسية
المتسلسلة الهندسية(E: Geometric Series)(T: Geometrik Seri ) وهي متسلسلة من الشكل:\[\sum^\infty_{k=1}…
المتسلسلة الريمانية
المتسلسلة الريمانية(E: Harmonic Series)(T: Harmonik Seri ) وهي متسلسلة من الشكل:\[\sum^\infty_{k=1}\…
العمليات على المتسلسلات
العمليات على المتسلسلات(E: Operations on Series)(T: Seriler Üzerinde İşlemler) لتكن لدينا المتسلسلتا…