الشكل الأسي للعدد العقدي
الشكل الأسي للعدد العقدي
(T: Karmaşık Sayıların Üstel Gösterimi)
(E: Exponential Representation of Complex Numbers)
ليكن لدينا العدد العقدي
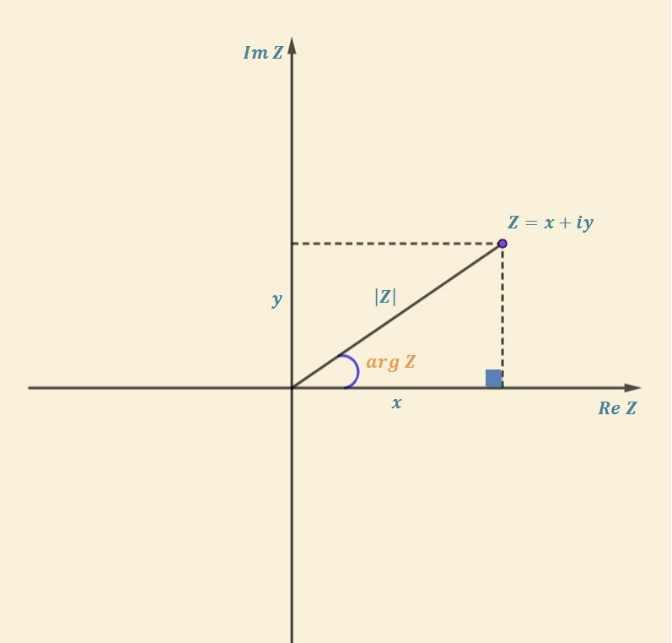
\[Z=x+iy\]
ولتكن \(|Z|\) طويلة العدد العقدي و \(arg Z\) سعة هذا العدد العقدي عندئذٍ وجدنا أنه يمكن كتابة العدد العقدي \(|Z|\) بالشكل المثلثي بالشكل التالي :
\[Z=r \left( \cos \theta +i \sin \theta\right)\]
وبحسب علاقة أولر (T: Euler Formülü) (E: Euler Formula):
$$ \bbox[5px,border:2px solid fuchsia]
{
e^{i\theta}= \cos \theta+i \sin \theta
}
$$
نجد أن:
\[Z=r \left( \cos \theta+i \sin \theta\right)\]
أي أن:
$$ \bbox[5px,border:2px solid fuchsia]
{
Z=re^{i\theta}
}
$$
وهو الشكل الأسي للعدد العقدي \(Z\) .
مثال: أوجد الشكل الأسي للعدد العقدي:
\[Z=1+1i\]
الحل:
\[r=|z|=\sqrt {x^2+y^2}=\sqrt {1^2+1^2}=\sqrt 2\]
\[argZ=\arctan (\frac{y}{x})=\arctan (\frac11)=\arctan (1)=\frac{\pi}{4}\]
وبالتالي:
\[Z=re^{i\theta}=\sqrt 2 e^\frac{\pi}{4}\]
وهو الشكل الأسي للعدد العقدي \(Z=1+1i\)
مقالات ذات صلة:
مجموعة الأعداد العقدية
الشكل الديكارتي للعدد العقدي
المعنى الهندسي للعدد العقدي
مرافق العدد العقدي
طويلة العدد العقدي
سعة العدد العقدي
الشكل المثلثي للعدد العقدي
معيار المقارنة للمتسلسلات
معيار المقارنة للمتسلسلات(E: The Comparison Test)(T: Karşılaştırma Testi) لتكن لدينا المتسلسلتان:\[\…
المعيار الصفري لتقارب متسلسلة
المعيار الصفري لتقارب متسلسلة لتكن لدينا المتسلسلة:\[\sum^\infty_{k=1}a_k\]إذا كان :\[\lim_{k \right…
المتسلسلة الهندسية
المتسلسلة الهندسية(E: Geometric Series)(T: Geometrik Seri ) وهي متسلسلة من الشكل:\[\sum^\infty_{k=1}…
المتسلسلة الريمانية
المتسلسلة الريمانية(E: Harmonic Series)(T: Harmonik Seri ) وهي متسلسلة من الشكل:\[\sum^\infty_{k=1}\…
العمليات على المتسلسلات
العمليات على المتسلسلات(E: Operations on Series)(T: Seriler Üzerinde İşlemler) لتكن لدينا المتسلسلتا…