نظرية البيان

تعريف البيان
(E: Graph)
(T: Graf)

يعرف البيان بأنه مجموعة من الرؤوس (E: Vertices) (T: Düğümler) ومجموعة من الأضلع (E:Edges) (T: Kenarlar) التي تربط هذه الرؤوس ببعضها البعض نرمز للبيان عادةً بالرمز \(G\) ونرمز لمجموعة الرؤوس بالرمز \(V\) ولمجموعة الأضلع بالرمز \(E\) . نرمز بالزوج \([u,v]\) لضلع البيان الواصل بين الرأس \(u\) والرأس \(v\) كما اننا نسمي الضلع \([u,u]\) الواصل بين الرأس \(u\) ونفسه لفة (E:Loop) (T: Döngü) ونقول عن رأسين \(u\) و \(v\) أنهما متجاورين (E: Adjancent) (T: Komşu) إذا وجد ضلع واصل بين \(u\) و \(v\) كما نقول عن ضلعين أنهما متجاوران إذا كانا مشتركان برأس.

مثال:

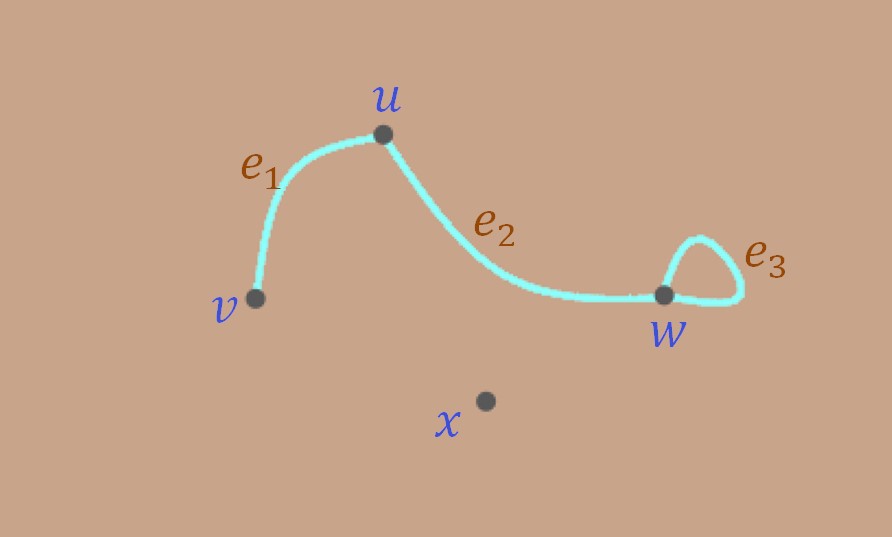
نلاحظ في البيان السابق أن مجموعة الرؤوس هي:
\[V=\{v,u,w,x\}\]
كما أن مجموعة الأضلاع هي:
\[E=\{[u,v],[u,w],[w,w]\}\] أو \[E=\{e_1,e_2,e_3\}\]
وتوجد لفة هي \([w.w]\) . إن الرأسين \(u\) و \(v\) متجاورين لأنهما مشتركان بضلع \(e_1\) كما أن الرأسين \(u\) و \(w\) متجاورين أيضاً لأنهما مشتركان بضلع \(e_2\) كما أن الضلعين \(e_1\) و \(e_2\) متجاوريين لأنهما مشتركان بالرأس \(u\).